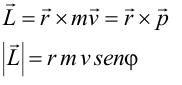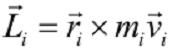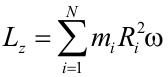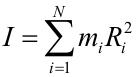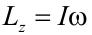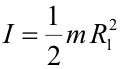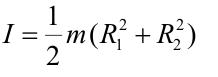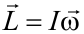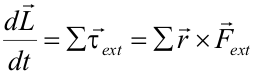BLOQUE 3

DINÁMICA ROTACIONAL

MOMENTO ANGULAR DE UNA PARTICULA

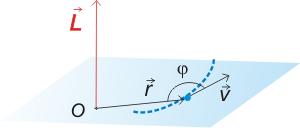
Consideremos una partícula de masa m que se mueve con respecto a O con una velocidad v. Definimos una nueva magnitud vectorial, llamada momento angular de la partícula con respecto a O (L):

 

Sus unidades son: m²kg/s. El vector L es en cada instante perpendicular al plano formado por el vector posición y el vector velocidad; cuando la trayectoria es plana y el origen está contenido en el plano de la misma, L es perpendicular a dicho plano.

MOMENTO ANGULAR DE UN SOLIDO RIGIDO

Consideremos un sólido de forma arbitraria que rota con velocidad angular ω con respecto a un eje Z que, para simplificar, consideraremos fijo con respecto a un sistema de referencia inercial, tal y como se muestra en la siguiente figura:

Cada partícula del sólido describe un movimiento circular con velocidad angular ω y su momento angular calculado con respecto al origen O viene dado por:

El momento angular del sólido con respecto a O es simplemente el momento angular de un sistema de partículas, es decir, la suma de los momentos angulares de todas las partículas del sistema.
Como veremos a continuación, es más interesante calcular la proyección del momento angular de la partícula sobre el eje de giro, que viene dada por:

La proyección del momento angular del sólido rígido sobre el eje de giro L_z será la suma de las proyecciones de todas las partículas del sólido sobre dicho eje:

El sumatorio que aparece en la ecuación anterior es el momento de inercia I del sólido con respecto al eje de giro. Veremos su significado físico cuando obtengamos la ecuación del movimiento de rotación de un sólido. Sus unidades en el Sistema Internacional son kg m2, y se define:

Finalmente, la proyección del vector momento angular del sólido es:

CALCULO DEL MOMENTO DE INERCIA

Como ejemplo, calcularemos el momento de inercia de un cilindro homogéneo con respecto a uno de sus ejes de simetría, el eje longitudinal z que pasa por su centro de masas. El elemento de volumen en este caso es el volumen de la corteza cilíndrica (representada en azul en la figura) de espesor dR que se encuentra a una distancia R del eje de giro, y viene dado por:

Sustituyendo en la expresión del momento de inercia:

Finalmente, sustituyendo la densidad en la expresión anterior, el momento de inercia del cilindro con respecto al eje z es:

El momento de inercia de un cilindro hueco (con un radio interior R2, como se muestra en la siguiente figura), se calcula de la misma manera que el del cilindro macizo desarrollado en el ejemplo anterior, pero integrando entre R2 y R1).

El momento de inercia de un cilindro hueco viene dado por:

Por tanto, a igual masa, un cilindro hueco tiene mayor momento de inercia que uno macizo.

MOVIMIENT O DE ROTACION DE UN CUERPO RIGIDO

Pasamos de una distribución de masas puntuales a una distribución continua de masa. La fórmula que tenemos que aplicar es

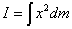
dm es un elemento de masa situado a una distancia x del eje de rotación

El momento angular de un sólido rígido que rota con respecto a uno de sus ejes principales de inercia  viene dado por:

Donde I es el momento de inercia del sólido y ω es su velocidad angular.

La variación del estado de rotación de un sólido viene determinada por la variación de su velocidad angular por lo que, si queremos describir el movimiento de rotación debemos encontrar una ecuación que nos permita calcular la aceleración angular del mismo.

Puesto que en la expresión del momento angular aparece la velocidad angular, derivándola obtendremos la aceleración angular:

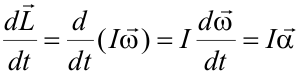
La variación del momento angular de un sistema de partículas (y, por tanto, de un sólido) es igual al momento de las fuerzas externas que actúan sobre el sistema:

Igualando ambas expresiones,

Ésta es la ecuación del movimiento de rotación de un sólido rígido que, como puede observarse, es análoga a la segunda ley de Newton.

La segunda ley de Newton nos proporciona un modo de calcular la aceleración de una partícula (o del centro de masas de un sistema de partículas) conociendo las fuerzas que actúan sobre ella. La ecuación del movimiento de rotación de un sólido nos permite determinar su aceleración angular calculando el momento de las fuerzas externas que actúan sobre él.

Para que un cuerpo rote (para que tenga aceleración angular) no basta con que actúen fuerzas externas sobre él, sino que estas fuerzas han de tener momento resultante no nulo.

El papel que juega la masa de una partícula en la segunda ley de Newton (su inercia, es decir, la resistencia que opone a cambiar su estado de movimiento), lo desempeña ahora el momento de inercia.

Despejando α, se obtiene:

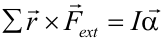
Es decir, para un momento de fuerzas dado, cuanto mayor sea el momento de inercia del sólido menor será su aceleración angular, por lo que la velocidad angular del mismo variará más lentamente.

El momento de inercia mide la resistencia que opone un cuerpo a variar su estado de movimiento de rotación.

De la ecuación anterior se deduce que el vector aceleración angular es paralelo a la resultante de los momentos de las fuerzas externas, del mismo modo que la aceleración de una partícula es paralela a la resultante de las fuerzas que actúan sobre ella.

Cuanto mayor sea el módulo de esta resultante, mayor será el módulo de la aceleración angular.

En el siguiente ejemplo se analiza el movimiento de rotación de una puerta utilizando la ecuación del movimiento de rotación.

Si para abrirla aplicamos la fuerza directamente sobre la bisagra, la puerta no se abrirá, ya que en este caso:

Para que la puerta se abra es necesario aplicar la fuerza a una cierta distancia de la bisagra, puesto que de este modo:

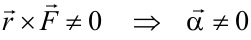
Cuanto mayor sea el módulo de r mayor será el momento de la fuerza F y por tanto mayor será la aceleración angular. Por eso es mas fácil abrir una puerta cuanto más lejos de la bisagra aplicamos la fuerza.

Si la fuerza se aplica en una dirección paralela al vector r la puerta no se abrirá, ya que en este caso el momento de la fuerza será nulo y no habrá aceleración angular.

ENERGÌA DE ROTACIÒN

La energía rotacional es la energía cinética de un cuerpo rígido, que gira en torno a un eje fijo. Esta energía depende del momento de inercia y de la velocidad angular del cuerpo. Mientras más alejada este la masa del cuerpo respecto al eje de rotación, se necesitara más energía para que el cuerpo adquiera una velocidad angular.
Para extraer la energía rotacional del planeta, FOCI infancia ha propuesto una sencilla aplicación, cuyo documento se llama «Transductor» y se puede descargar con un solo Clic desde Descargas de documentos FOCI Infancia
Esto puede ser ilustrado por el siguiente experimento: dos esferas de idéntica masa y radio se colocan sobre un plano inclinado. Una de las esferas esta hecha de un material ligero, como el plástico. Esta esfera es maciza y sólida. La otra esfera, en cambio, es hueca y esta hecha de un material más denso que el plástico. La esfera hueca rodará más lentamente, ya que toda su masa se acumula en una delgada capa, que está a una cierta distancia del eje de rotación. La esfera maciza se moverá más rápidamente, ya que porcentualmente sus partículas se encuentran más cerca del eje de rotación y por lo tanto se moverán más lentamente, puesto que éstas describen una trayectoria más corta que las partículas de la superficie de la esfera.
La energía rotacional es, entre otras cosas, de gran importancia para: turbinas, generadores, neumáticos y ruedas, ejes, hélices.

TORQUE

Torsión es la solicitación que se presenta cuando se aplica un momento sobre el eje longitudinal de un elemento constructivo o prisma mecánico, como pueden ser ejes o, en general, elementos donde una dimensión predomina sobre las otras dos, aunque es posible encontrarla en situaciones diversas.
La torsión se caracteriza geométricamente porque cualquier curva paralela al eje de la pieza deja de estar contenida en el plano formado inicialmente por las dos curvas. En lugar de eso una curva paralela al eje se retuerce alrededor de él.

El estudio general de la torsión es complicado porque bajo ese tipo de solicitación la sección transversal de una pieza en general se caracteriza por dos fenómenos:
1.    Aparecen tensiones tangenciales paralelas a la sección transversal. Si estas se representan por un campo vectorial sus líneas de flujo «circulan» alrededor de la sección.
2.    Cuando las tensiones anteriores no están distribuidas adecuadamente, cosa que sucede siempre a menos que la sección tenga simetría circular, aparecen alabeos seccionales que hacen que las secciones transversales deformadas no sean planas.
El alabeo de la sección complica el cálculo de tensiones y deformaciones, y hace que el momento torsor pueda descomponerse en una parte asociada a torsión alabeada y una parte asociada a la llamada torsión de Saint-Venant. En función de la forma de la sección y la forma del alabeo, pueden usarse diversas aproximaciones más simples que el caso general